
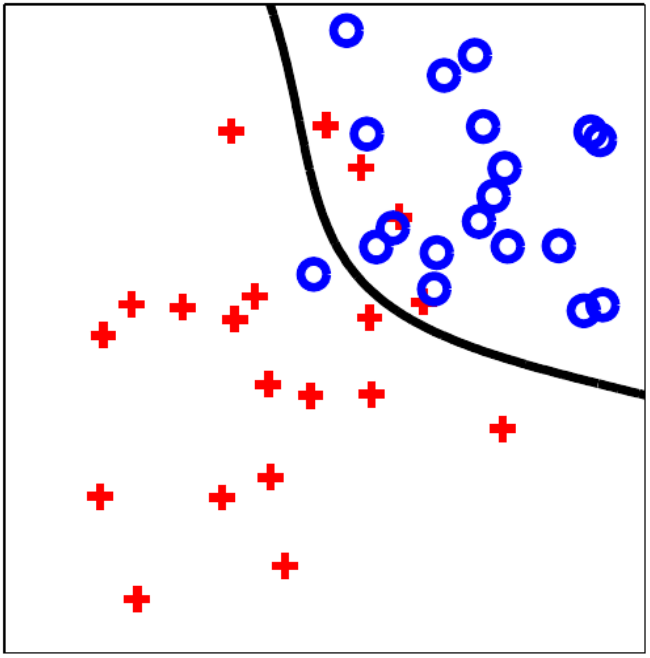
For example, if A is a closed half plane and B is bounded by one arm of a hyperbola, then there is no separating hyperplane:Ī = A more subtle counterexample is one in which A and B are both closed but neither one is compact. For example, A and B could be concentric circles. If one of A or B is not convex, then there are many possible counterexamples. The theorem does not apply if one of the bodies is not convex. See the article on Support Vector Machines for more details. The margin between the hyperplane and the clouds is maximal. In geometry, a maximum-margin hyperplane is a hyperplane which separates two 'clouds' of points and is at equal distance from the two.
The Hahn–Banach separation theorem generalizes the result to topological vector spaces.Ī related result is the supporting hyperplane theorem. The hyperplane separation theorem is due to Hermann Minkowski. An axis which is orthogonal to a separating hyperplane is a separating axis, because the orthogonal projections of the convex bodies onto the axis are disjoint. In the second version, if both disjoint convex sets are open, then there is a hyperplane in between them, but not necessarily any gap.
In the first version of the theorem, if both these sets are closed and at least one of them is compact, then there is a hyperplane in between them and even two parallel hyperplanes in between them separated by a gap. In geometry, the hyperplane separation theorem is either of two theorems about disjoint convex sets in n-dimensional Euclidean space. ISBN 0-7923-9821-1.Illustration of the hyperplane separation theorem. Nondifferentiable and two-level mathematical programming. Shimizu, Kiyotaka Ishizuka, Yo Bard, Jonathan F.Modified Lagrangians and monotone maps in optimization. ^ Haïm Brezis, Analyse fonctionnelle : théorie et applications, 1983, remarque 4, p.^ Boyd & Vandenberghe 2004, Exercise 2.22.Data Mining: Practical Machine Learning Tools and Techniques (Fourth ed.). The Elements of Statistical Learning : Data Mining, Inference, and Prediction (PDF) (Second ed.). ^ Hastie, Trevor Tibshirani, Robert Friedman, Jerome (2008).įor increased efficiency, parallel axes may be calculated as a single axis. Additional axes, consisting of the cross-products of pairs of edges, one taken from each object, are required. In 3D, using face normals alone will fail to separate some edge-on-edge non-colliding cases. Note that this yields possible separating axes, not separating lines/planes. Each face's normal or other feature direction is used as a separating axis. The separating axis theorem can be applied for fast collision detection between polygon meshes. Regardless of dimensionality, the separating axis is always a line.įor example, in 3D, the space is separated by planes, but the separating axis is perpendicular to the separating plane. SAT suggests an algorithm for testing whether two convex solids intersect or not. Two convex objects do not overlap if there exists a line (called axis) onto which the two objects' projections do not overlap. The separating axis theorem (SAT) says that: Technically a separating axis is never unique because it can be translated in the second version of the theorem, a separating axis can be unique up to translation.
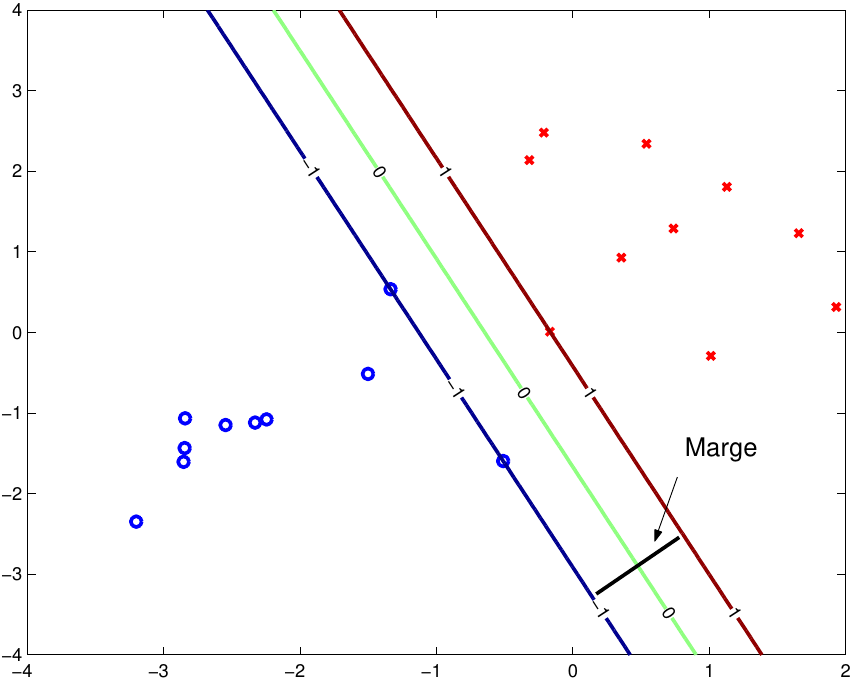
In the second version, it may or may not be unique. In the first version of the theorem, evidently the separating hyperplane is never unique. For example, A can be a closed square and B can be an open square that touches A. (Although, by an instance of the second theorem, there is a hyperplane that separates their interiors.) Another type of counterexample has A compact and B open. In the context of support-vector machines, the optimally separating hyperplane or maximum-margin hyperplane is a hyperplane which separates two convex hulls of points and is equidistant from the two. In another version, if both disjoint convex sets are open, then there is a hyperplane in between them, but not necessarily any gap. In one version of the theorem, if both these sets are closed and at least one of them is compact, then there is a hyperplane in between them and even two parallel hyperplanes in between them separated by a gap. There are several rather similar versions. In geometry, the hyperplane separation theorem is a theorem about disjoint convex sets in n-dimensional Euclidean space.


 0 kommentar(er)
0 kommentar(er)
